Kernel Density Estimation

Why KDE?

Source

https://scikit-learn.org/stable/modules/density.html

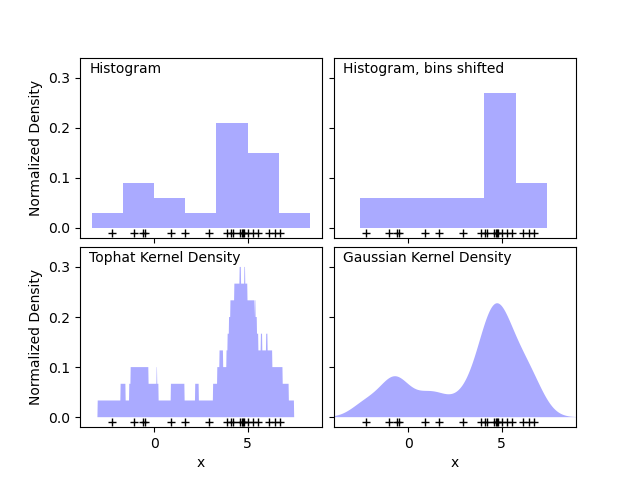
A major problem with histograms, however, is that the choice of binning can have a disproportionate effect on the resulting visualization.

Intuitively, one can also think of a histogram as a stack of blocks, one block per point. By stacking the blocks in the appropriate grid space, we recover the histogram.

But KDE is better because, instead of stacking the blocks on a regular grid, it centers each block on the point it represents, and sums the total height at each location.

Math

Mathematically, a kernel is a positive function $K (x; h)$ which is controlled by the bandwidth parameter $h$ . Given this kernel form, the density estimate at a point $y$ within a group of points $x_{i}; i = 1 . . . N$ is given by:

p κ (y) = \sum^{N} K (y - x_{i}; h)

Free parameters of kernel density estimation:

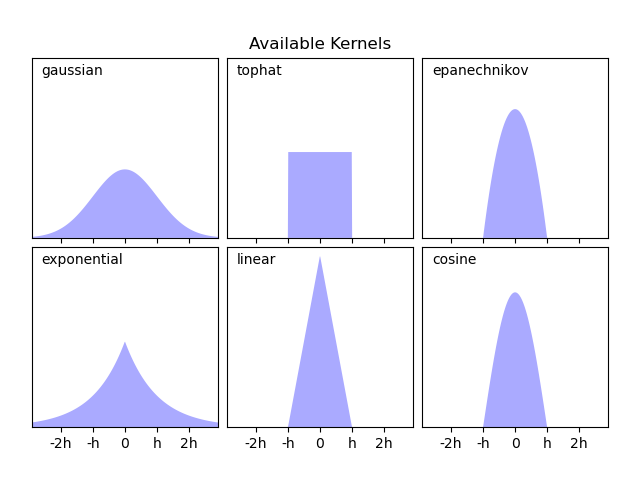
kernel, which specifies the shape of the distribution placed at each point
kernel bandwidth, which controls the size of the kernel at each point. It acts as a smoothing parameter, controlling the tradeoff between bias and variance in the result. A large bandwidth leads to a very smooth (i.e. high-bias) density distribution. A small bandwidth leads to an unsmooth (i.e. high-variance) density distribution.

Why KDE?

Math

Types of Kernels